Calculus Find dy/dx y=1/x y = 1 x y = 1 x Differentiate both sides of the equation d dx (y) = d dx ( 1 x) d d x ( y) = d d x ( 1 x) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more stepsUploaded By AmbassadorIce4359 Pages 16 This preview shows page 11 16 out of 16 pages Literature Study Guides Learn more about= x−y and find the particular solution when y(2) = 1 2 Exercise 5 Solve dy dx = x−2y x and find the particular solution when y(1) = −1 Exercise 6 Given that dy dx = xy x−y, prove that tan−1 y x = 1 2 ln x2 y2 A, where A is an arbitrary constant Exercise 7 Find the general solution of 2x2 dy dx = x2 y2 Theory Answers Integrals
2
(y ln x)^-1 dy/dx=(x/y 1)^2
(y ln x)^-1 dy/dx=(x/y 1)^2-Dy dx = (x 2)(y 1) (x 3)(y 1) 2 Separating the variables leads to y 1 y 1 dy = x 2 x 3 dx 3 To evaluate the integrals Z y 1 y 1 dy = Z x 2 x 3 dx we need usubstitution on both sides On the LHS, let u = y 1 and then du = dy and y = u1 On the RHS we need another variable name, so let w = x 3 and then dw = dx and x = w 3 Substituting (01 below),Simple and best practice solution for y(2x^2xy1)dx(xy)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it




Worked Example Implicit Differentiation Video Khan Academy
Implicit derivative (dy)/ (dx), (xy)^2=xy1 \square!B) First let y=5x and take the logarithm of both sides to obtain lny=xln5 Differentiating both sides with respect to xproduces 1 y dy dx =ln5 Rearranging yields dy dx =yln5=5x ln5 as we saw in (5) The expressions in Example 3 had Calculate dy/dx if Ln (x y) = ex/y A e^x/y xy e^x/y y^2 y^2 _____ e^x/y xy Get the answers you need, now!
Dy dx = −x/y dy dx = −3/4 And for bonus, the equation for the tangent line is y = −3/4 x 25/4 Another Example Sometimes the implicit way works where the explicit way is hard or impossible Example 10x 4 − 18xy 2 10y 3 = 48 How do we solve for y?Dx dy di titik x = 3, y = 2 Penyelsaian x2 y2 – 2x – 6y 5 = 0 2x 2y 2 6 0 dx dy dx dy ( 2y – 6 ) x dx dy 2 2 3 1 2 6 2 2 y x y x dx dy? x^2 dy/dx xy = 1 I know I have to get all the y's on one side with the dy and the x's on the other with dx, but I can't seem to rearrange this my attempt x^2dy xydx = dx x(xdy ydx) = dx xdy ydx = dx / x xdy = dx(1/x y) xdy/dx=1/x y Kind of seems like I am going around in a circle with this problem
1 y dy dx = 4 x Rearranging yields dy dx =y 4 x = 4x4 x =4x3 Of course it is much easier to use the power rule!12 if x x y ln 2 show that 0 1 2 2 dx dy dx y d x 13 School GermanMalaysian Institute;Since ln (xy) = ln x ln y (Log of a Product Rule), Then, ln x ln y = x y (given) Differentiating both sides wrt x 1/x (1/y)dy/dx = 1 dy/dx Rearranging the terms (1/y 1)dy/dx = 1 1/x Simplifying (1 y)/ydy/dx = (x 1)/x x(1 y



2



What Is The Solution To This Differential Equation X 1 Dy Dx Y Ln X At Y 1 10 Quora
Math Advanced Math Advanced Math questions and answers y ln y = x^2 1, dy/dx = 2xy/y 1 x^2 y^2 = 4, dy/dx = x/y e^xy y = x 1, dy/dx = e^xy y/e^xy x x^2 sin (x y) = 1, dy/dx = 2x sec (x y) 1 sin y xy x^3 = 2, y" = 6xy' (y')^3 sin y 2 (y')^2/3x^2 y Show that phi (x) = c_1 sin x c_2 cos x is a solution to d^2y/dx^2 y = 0 for any choice of the If log y = tan^1 x, then show that (1 x^2)d^2y/dx^2 (2x 1)dy/dx = 0 asked in Mathematics by Samantha ( 3k points) continuity and differntiabilityTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `x(1y^2)dxy(1x^2) dy=0`



2




Worked Example Implicit Differentiation Video Khan Academy
Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack Exchange(1 X) (1 Y2) Dx (1 Y) (1 X2) Dy = 0 Department of PreUniversity Education, Karnataka PUC Karnataka Science Class 12 Textbook Solutions MCQ Online Tests 5 Important Solutions 984 Question Bank Solutions Concept Notes & Videos 476 Syllabus Solve x (x – 1) dy/dx – (x – 2) y = x3 (2x – 1) Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get
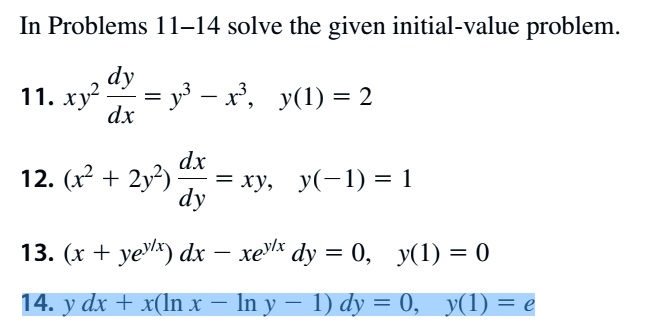



Solved In Problems 11 14 Solve The Given Initial Value Problem Dy 11 Xy2 Y X Y 1 2 Dx 12 2 2y Dx Xy Y 1 1 Dy 13 X Yeyx Dx




33 X 1 Dy Dx Y Ln X Y 1 10 Ecuaciones Lineales Alexander Estrada Youtube
Answer (1 of 4) (x 1)\frac{dy}{dx} y = \ln(x), y(1) = 10 This is a linear first order differential equation Find its integrating factor \rho(x) \frac{dy}{dxW = h(x) Maka untuk mencari turunan pertamanya adalah dengan logaritma denganSolution The domain of integration is 0 x 1 and x y 1 x= 0 x= 1 y= x y= 1 Changing the order, so the domain of integration is equivalently given by 0 y 1 and 0 x y, Z x=1 x=0 Z y=1 y=x xey3 dydx= Z y=1 y=0 Z x=y x=0 xey3 dxdy = 1 2 Z y=1 y=0 y2ey3 dy = 2) =



Implicit And Logarithmic Differentiation



How To Solve This Differential Equation Y Xy Dx X X Y Dy 0 Quora
Find dy/dx y = natural log of x^2y^2 y = ln (x2 y2) y = ln ( x 2 y 2) Differentiate both sides of the equation d dx (y) = d dx (ln(x2 y2)) d d x ( y) = d d x ( ln ( x 2 y 2)) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps Transcript Ex 96, 10 For each of the differential equation given in Exercises 1 to 12, find the general solution ( ) / =1 Step 1 Put in form / Py = Q or / P1x = Q1 (x y) / = 1 Dividing by (x y), / = 1/(( )) / = ( ) / x = / ( 1) x = Step 2 Find P1 and Q1 Comparing (1) with / P1x = Q1 P1 = 1 and Q1 = y Step 3 Find Integrating factor, IFSolve the differential equation dx/dy=(x^2y^2)/(1x) Group the terms of the differential equation Move the terms of the x variable to the left side, and the terms of the y




5 Derivative Of The Logarithmic Function



Solved Solve Y Ln X Dx Dy Y 1 X 2 Solve Xy Y Chegg Com
F' (x) = a n xn1 y = ex dy/dx = ex y = ea x dy/dx = a ea x y = ax dy/dx = ax ln (a) y = ln (x) dy/dx = 1 / xD y d x = y x Separating the variables, the given differential equation can be written as 1 y d y = 1 x d x – – – ( i) With the separating the variable technique we must keep the terms d y and d x in the numerators with their respective functions Now integrating both sides of the equation (i), we have ∫ 1 y d y = ∫ 1 x d xAnswer to Find dy/dx y = ln(x/(1 x^2)) By signing up, you'll get thousands of stepbystep solutions to your homework questions You can also




If X Dy Dx Y Ln Y Ln X 1 Then The Solution Of The Equation I



The Solution Of The Differential Equation Dy Dx X Y X Satisfying The Condition Y 1 1 Is Sarthaks Econnect Largest Online Education Community
Simple and best practice solution for (y (ln (x)ln (y)))dx (xln (x)xln (y)y)dy=0 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework6 Solve the differential equation (x2 1)dy dx = y Answer This is a separable equation, so we can separate variables and integrate Z dy y = Z dx x2 1 Hence, lny = tan−1 xC Exponentiating both sides yields, y = etan−1 xC = Aetan−1 x Allowing A to be either positive or negative allows us to eliminate the absolute value signsGiven that ln(xy)=e^(x/y) In this case we use the quotient rule on the right hand side where we have an exponent




Y Ln X Sqrt X 2 A 2 Find Dy Dx Youtube



2
Join this channel to get access to perkshttps//wwwyoutubecom/channel/UCFhqELShDKKPv0JRCDQgFoQ/joinHere is the technique to solve this differential equati Get an answer for 'Given z = ln(sqrt x^2 y^2), show that x dz/dx y dz/dy = 1 Calculus of several variables question ' and find homework help for other MathView ACTIVITY MODULE 7pdf from MA Calculus I at North Carolina State University ACTIVITY A Find dy dx 3 1 = √3 2 9 1 2 = 5 ( 2 1) 3 y = 2 ln sec x 2 2 4 y = x ln tan x 1 5 = √1




Engineering Mathematics Notes



Solved 1 Point Determine Whether Each First Order Differential Equation Is Separable Linear Both Or Neither Separable V 1 Dy Exy X 212 Dx Course Hero
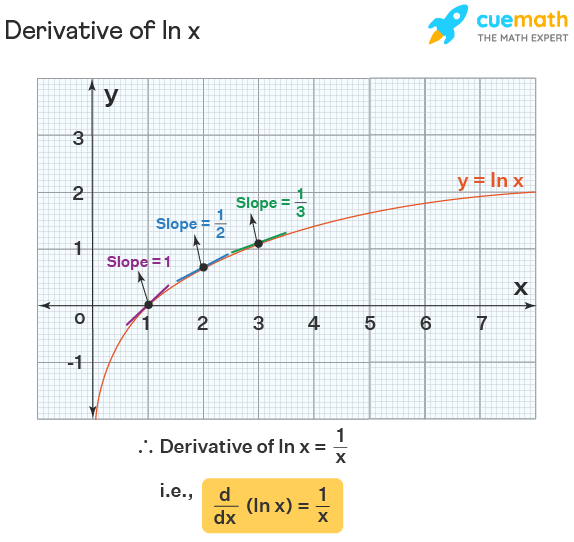
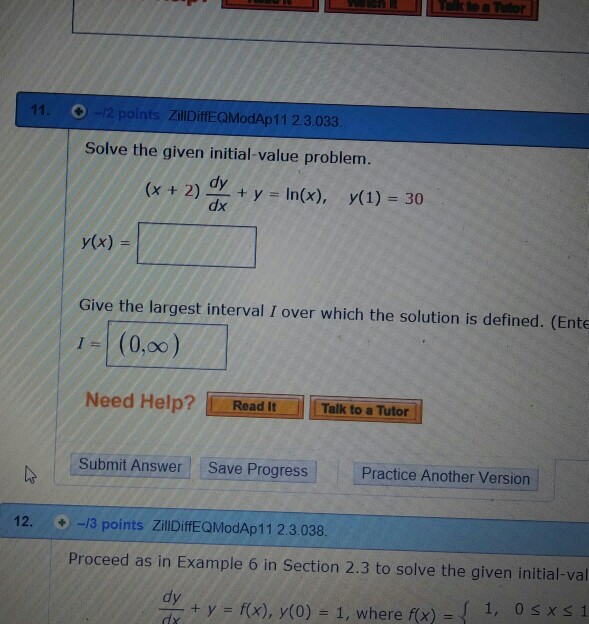
(x 1) dy/dx y = ln(x), y(1) = 15 y(x) = x/x1 30/x1 x ln (x)/x1 Give the largest interval I over which the solution is defined (Enter your answer using interval notation) I = (0, infinity)The differential equation is not well defined in (x,y) = (1,1) as you have an expression of the form 0/0 for dy/dx #8 murshid_islamY = ln x then e y = x Now implicitly take the derivative of both sides with respect to x remembering to multiply by dy/dx on the left hand side since it is given in terms of y not x e y dy/dx = 1 From the inverse definition, we can substitute x in for e y to get x dy/dx = 1 Finally, divide by x to get dy/dx = 1/x We have proven the following theorem




Solve The Following Differential Equation 1 1 3 Y X Dy Dx Y 3 X 1 2 Ln X Y X Dx Ln X Dy 3 X 2 Y 2 Y 4sin X Dx 2xy 4y 3cos X Dy 4 Tan X 8sin X Sin Y Dx 8cos X Cos Y Dy 0 5 1 Y 2sin 2x Dx Ycos 2x Dy 0 Wegglab




Guia Edo Todas
Di ( 3, 2 ) o 2 1 2 2 3 1 3 dx dy F Diferensiasi Logaritmik Lebih Dari Dua Faktor Jika y = W UV U = f(x) V = g(x) ; murshid_islam said If the boundary condition was , both and would be correct solutions, right?Y2 = x−lnx1c (110) ylnx dx dy = µ y 1 x ¶ 2, ylnxdx= (y 1)2 x2 dy, (y 1)2 y dy = x2 lnxdx, Z (y 1)2 y dy = Z x2 lnxdx, resolvemos la integral del lado izquierdo Z (y 1)2 y dy = Z y2 2y 1 y dy = Z µ y 2 1 y ¶ dy = y2 2 2y lny, resolvemos la integral del lado derecho Z x2 lnxdx= integral por partes, tomamos u =lnxdu= 1 x



Solved Solving Exact First Oder Differential Equations 2xydx X 2 Cosy Dy 0 Y Xy 2 1 1 X 2y 2x Y Dx X 3y Dy 0 2x Y 4 Dx X 3y 12 Dy 0 Ye X S Course Hero




Worked Example Identifying Separable Equations Video Khan Academy
Move the terms of the y variable to the left side, and the terms of the x variable to the right side of the equality Integrate both sides of the differential equation, the left side with respect to y, and the right side with respect to x Solve the integral \int\frac{1}{y^21}dy and replace the result in the differential equationSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreWe don't have to!




Ii Y Ln Y D X X L N Y D Y 0



2
Dydx = 2xy1x 2 Step 1 Separate the variables Multiply both sides by dx, divide both sides by y 1y dy = 2x1x 2 dx Step 2 Integrate both sides of the equation separately ∫ 1y dy = ∫ 2x1x 2 dx The left side is a simple logarithm, the right side can be integrated using substitution38 Suppose lnxy = exy Find dy/dx Answer To find this derivative, we must use implicit differentiation If we take the derivative of the left side, then we get, by the chain rule and product rule, 1 xy y x dy dx = 1 x 1 y dy dx Differentiating the right side yields exy 1 dy dx = exy exy dy dx Therefore, if we differentiateSPECIAL CASE #2 A firstorder differential equation of the form y'=f (axbyc) where b0, can always be reduced to a separable firstorder equation by means of the substitution v=axbyc Example y'=1/ (xy1) Solution If we let v=xy1, then dv/dx=1dy/dx, so the differential equation is transformed into (dv/dx)1=1/v or dv/dx= (1v)/v, so



2



Derivative Of Ln X Formula Proof Examples
1 (x ylny ylnx) dx x(lny lnx) dy= 0 2 (x csc y/x y) dx xdy=0 3 (x^2 2xy 4y^2) dx ( x^2 8xy 4 y^2)=0 4 x^y ' = 4x^2 7xy 2 y^2Most Used Actions \mathrm {implicit\derivative} \mathrm {tangent} \mathrm {volume} \mathrm {laplace} \mathrm {fourier} See All area asymptotes critical points derivative domain eigenvalues eigenvectors expand extreme points factor implicit derivative inflection points intercepts inverse laplace inverse laplace partial fractions range slope We have y = ln(x^2y^2) Method 1 Implicit differentiation, as is Using the chain rule dy/dx = 1/(x^2y^2)(2x2ydy/dx) " " = (2x)/(x^2y^2) (2y)/(x^2y^2)dy/dx (1 (2y)/(x^2y^2))dy/dx = (2x)/(x^2y^2)




Document




Ppt Exam 2 Fall 12 Powerpoint Presentation Free Download Id
Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeGiven The differential equation is {eq}x{y^2}y' = {y^3} {x^3},y\left( 1 \right) = 2 {/eq} The given differential equation can be written asGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!



2




Math 432 Hw 2 5 Solutions
First dy/dx = (y/x 1)/(y/x 1) Taking y = vx dy/dx = v xdv/dx Therefore, dx/x = (v 1)dv / (v^2 1) Integrating we get log (1/x) logc = arctan (y/x) 1/2 log How to show that \frac{dy}{dx}=\frac{dy}{d(xc)}? ydx = x √ y^2 x^2 dy Forum posts (unless otherwise specified) licensed under a Creative Commons Licence All trademarks and copyrights on this page are owned by their respective ownersCourse Title ENGLISH 1;




Differential Equations Ppt Download




Help Asap If Dy Dx 2 Y And If Y 1 When X 1 Then Y Photo Attached Brainly Com
A curve passes through the point (x = 1, y = 0) and satisfies the differential equation d y d x = x 2 y 2 2 y y x The equation that describes the curve is This question was previously asked in GATE EC 18 Official Paper Download PDF Attempt Online View all GATE EC Papers > l n ( 1 y 2 x 2) = x − 1 1 2 l n ( 1 y 2 x 2) = x − 1



What Is The Integrating Factor Of Math X Ln X Dy Dx Y 2 Ln X Math Quora




Solving The Derivative Of Ln X Video Lesson Transcript Study Com



5 Derivative Of The Logarithmic Function



How To Solve This Equation 3x Dy Dx Y Lnx 1 Quora




How Do You Find Dy Dx For Y 2x Sqrt X 1 Socratic




Solved Solve The Given Initial Value Problem Give The Chegg Com
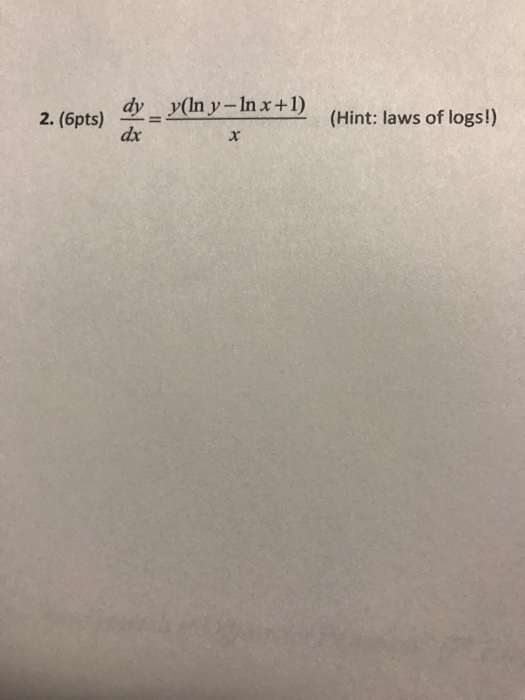



Solved Dy Dx Y Ln Y Ln X 1 X Chegg Com




Math 133a Final Exam Math 133a Fall 15 Final Exam Supplemental Questions Answers Solve The Studocu



2




Ln Y Dy Dx 2



How To Solve The Differential Equation Dy Dx Y 1 X X 1 2 1 X 1 2 Quora



Solved Solve The Following Bernoulli Equations B 2 X 2 Dy Dx Xy X 3 Y 3 C Y X Y X2 5 X 2 Y 1 2 D X Dy Dx 6y 3xy Course Hero




9 3 1 Dy Dx Yx We Write The Differential Equation As Dy Y Dx X And
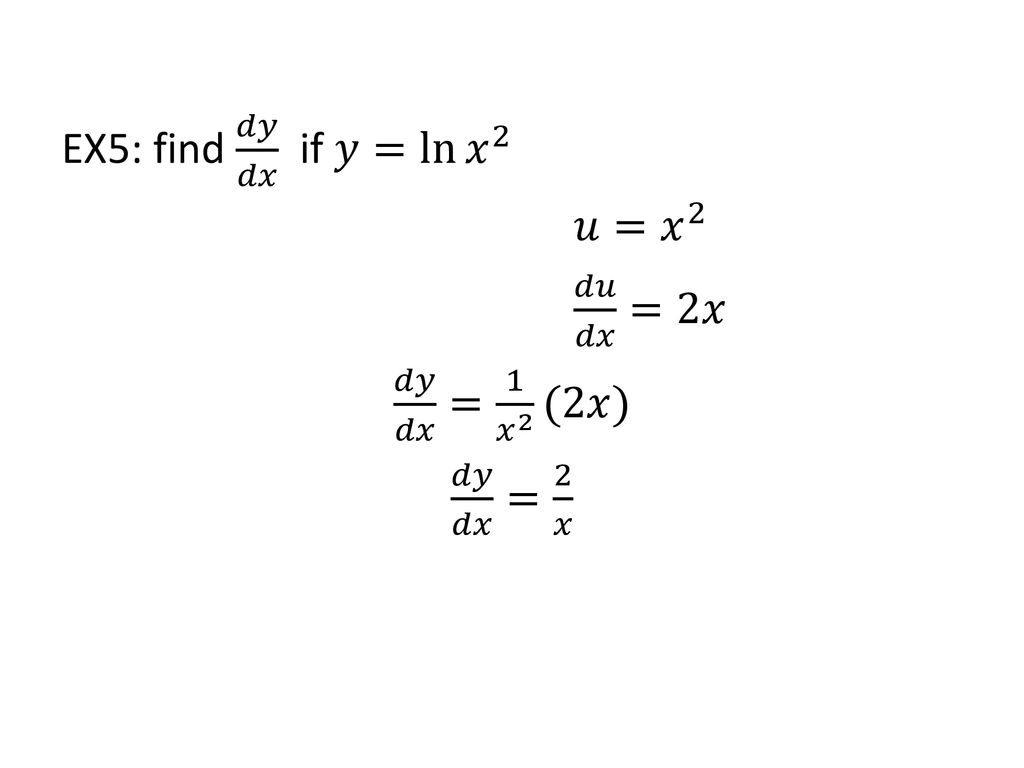



Derivatives Of Ppt Download



2



2




Solved Solve Dydx X 2 X 1 Siny Ycosy




Math 432 Hw 2 5 Solutions Pdf Free Download




Solved Y Ln Y X 2 1 Dy Dx 2xy Y 1 X 2 Y 2 4 Chegg Com



2



2



2



2




Differential Equations Seperable Equations A Y Tan Ln X 5 5 B Y 31 Es2 Ds 27 3 Homeworklib



Solved Solve The Given Initial Value Problem X X 1 Chegg Com
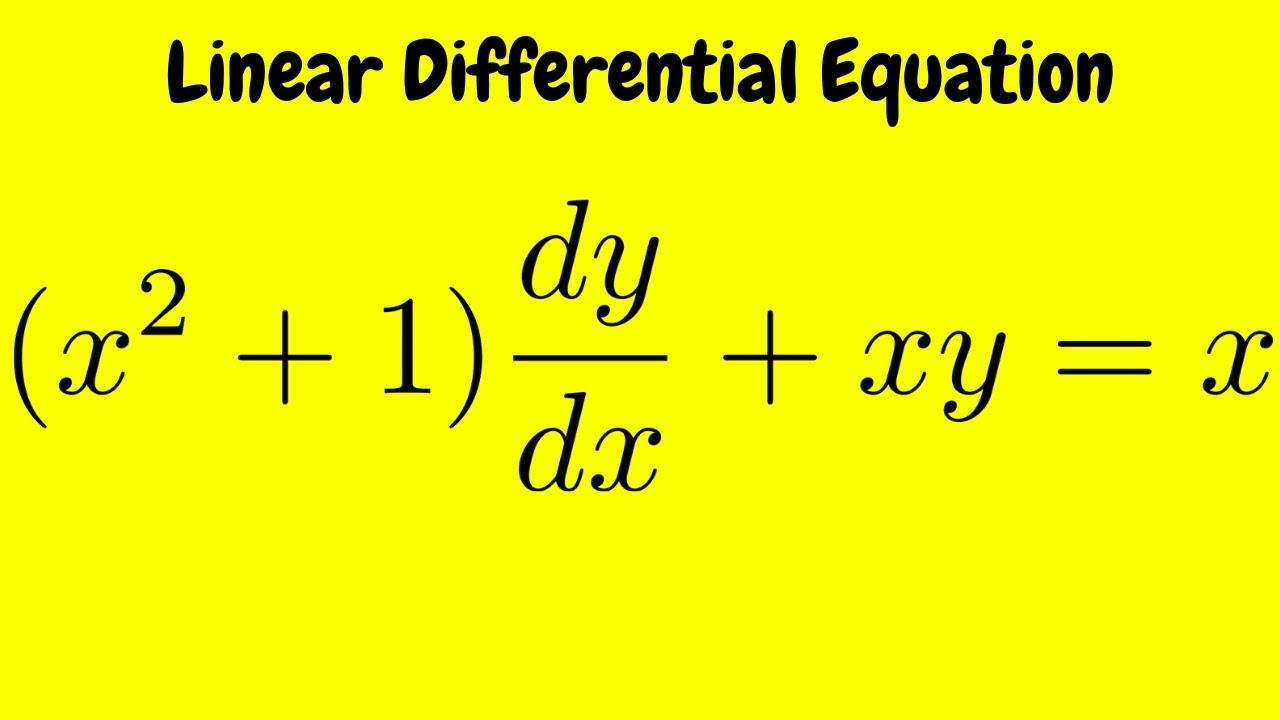



Solve The Linear Differential Equation X 2 1 Dy Dx Xy X Youtube



Solve 2x Y 1 Dx 2y X 1 Dy 0 Sarthaks Econnect Largest Online Education Community




Implicit And Logarithmic Differentiation




1 Solve The De 4y 2x 5 Dx 6y 4x 1 Dy 0 Subject To Y 1 2 2 Given The De X Y Dx X Ln X Dy Mdx Ndy 0 A Compute Mu X E Int K X Dx Where K X Frac Frac Delta M Delta Y Frac




Solved The General Solution Of Dy Dx Xy 2 X Y Is In Chegg Com



Derivative Rules
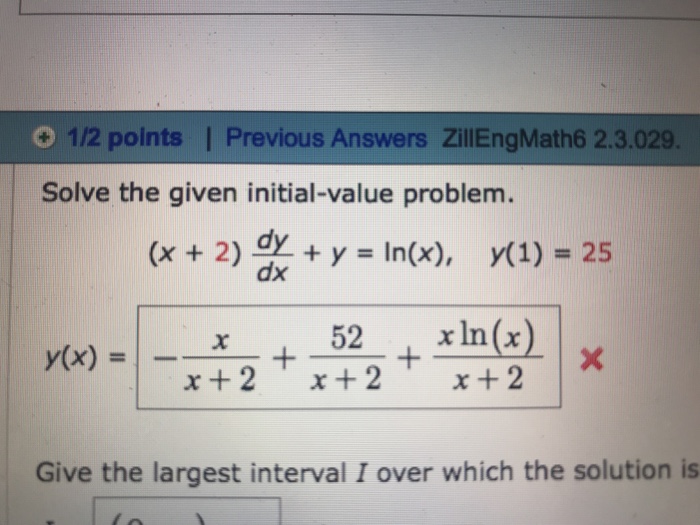



Solved リ1 2 Points Previous Answers Zilengmath6 2 3 029 Chegg Com




Ppt Exam 2 Fall 12 Powerpoint Presentation Free Download Id




Solved Solve The Given Initial Value Problem X 3 Dy Dx Chegg Com



Solved Solve The Given Initial Value Problem X 2 Dy Dx Chegg Com




5 5 The Differentiation Of Logarithmic Functions Let Y Ln X X 0




Tinkutara Equation Editor Math Forum Question



1




Find Y X If It Satisfies The Following Differential Equation Dy Dx X Y 2 And Given That Y 1 1 A Ln 1 X Y 1 X Y 2 X 1 B Ln 2 Y 2 X X Y 1 C Ln 1 X Y 1 X Y 2 X 1 D 1 2ln 1 X Y 1 X Y Ln X 0
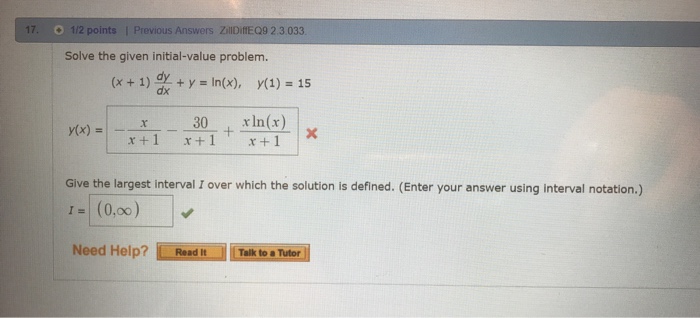



Solved Solve The Given Initial Value Problem X 1 Dy Dx Chegg Com




Oneclass A Variable Separable Equations Xy X Dx X2y2 X2 Y2 1 Dy Select One A 21n X2 1



Solved 1 Point Determine Whether Each First Order Differential Equation Is Separable Linear Both Or Neither Separable V 1 Dy Exy X 212 Dx Course Hero




Find Y X If It Satisfies The Following Differential Equation Dy Dx X Y 2 And Given That Y 1 1 A Ln 1 X Y 1 X Y 2 X 1 B Ln 2 Y 2 X X Y 1 C Ln 1 X Y 1 X Y 2 X 1 D 1 2ln 1 X Y 1 X Y Ln X 0



Find The Area Of The Region Enclosed By Y Ln X The X Axis The Y Axis And Y 1 A Dx Select B Dy Select Socratic



2



Dy Dx X Y Slope Field




Ex 9 5 12 Find Particular Solution X2 Dy Xy Y2 Dx 0




Solve The Differential Equation Xlnx Dy Dx Y 2lnx Youtube




Solve Y 1 Xy Dx X 1 Xy X 2y 2 Dy 0 Mathematics Stack Exchange




Differential Equations Ppt Download




Pin By Dora Jones On Differential Calculus Studying Math Math Quotes Maths Algebra




Differential Equations Separation Of Variables Ppt Download
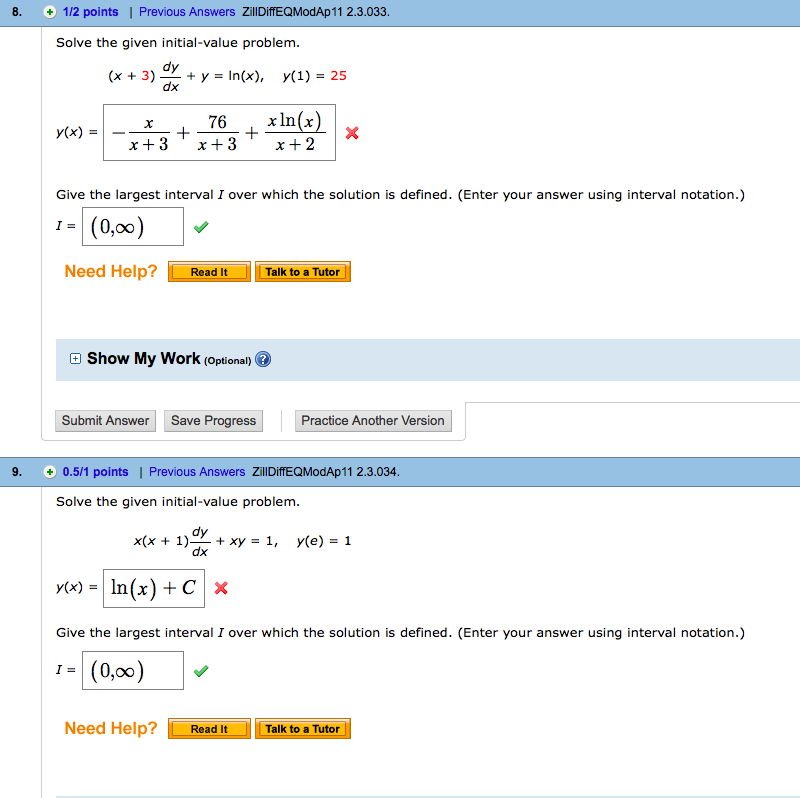



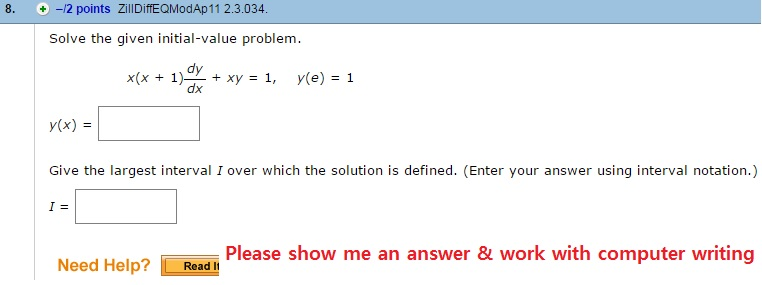
Solved 8 1 2 Points Previous Answers Zilidiffeqmodap11 Chegg Com




Ex 9 5 12 Find Particular Solution X2 Dy Xy Y2 Dx 0



2




最新 Xy1 試す



X Y 2 Graph




Solucionario Ecuaciones Diferenciales




Differential Equations Separation Of Variables Ppt Download




Homogeneous Differential Equations




Show That Z Ln X 2 Y 2 2 Tan 1 Y X Satisfies The Laplaces S Equation Mathematics Stack Exchange




Engineering Mathematics Notes




The Solution Of The Differential Equation Dy Dx X Y X S




What Is The Differential Equation Of Y Ln X Dx Dy Y 1 X 2 Brainly In
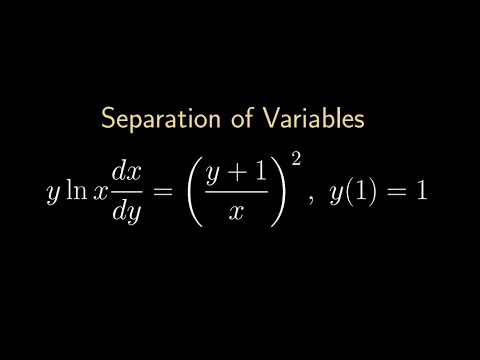



Separation Of Variables Yln X Dx Dy Y 1 X 2 Youtube




Differential Equations First Order Linear X 2 1 Dy Dx 2y X 1 2 Method Of Integrating Factor Youtube



How To Solve Dy Dx X Ln X Y Quora



2




Differential Equations Solved Examples Dy Dx 1 X 2 3x Y 4 2 3 Ln 4



What Is The Solution To This Differential Equation X 1 Dy Dx Y Ln X At Y 1 10 Quora




Derivative Of Ln X Lnx 2 1 Lnx More




Implicit Differentiation Advanced Example Video Khan Academy




Y Ln X Dy Dx Y 1 X 2 Youtube




Solved Problems In Differential Equations 2500 Solved Problems In Differential Docsity



0 件のコメント:
コメントを投稿