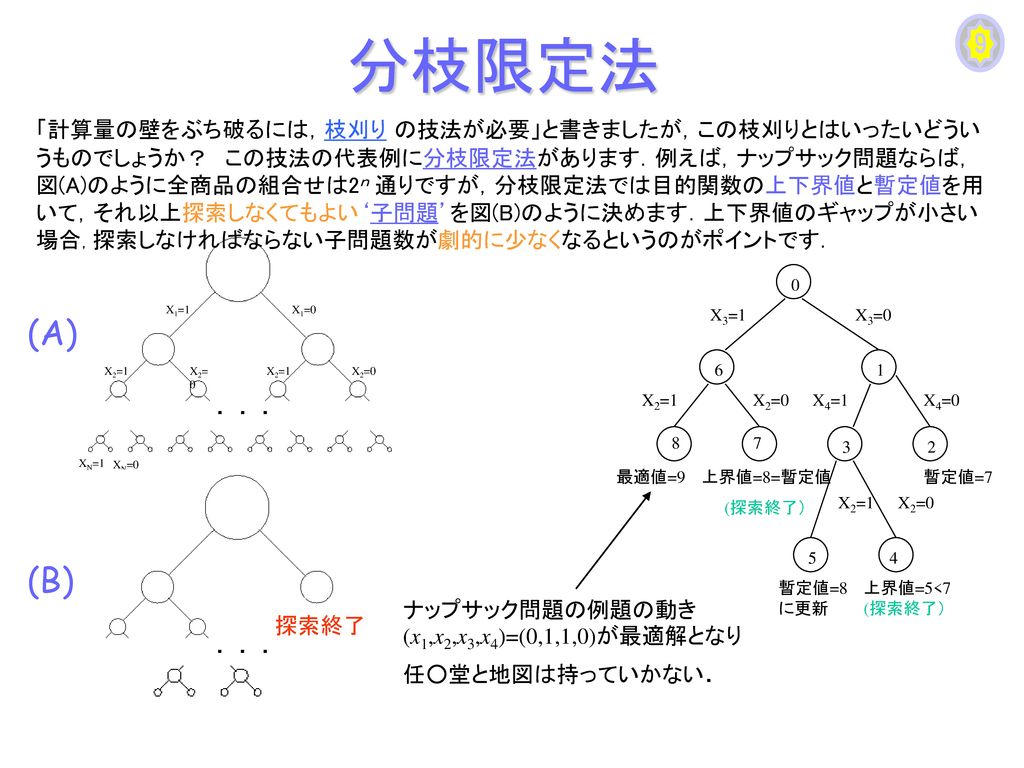
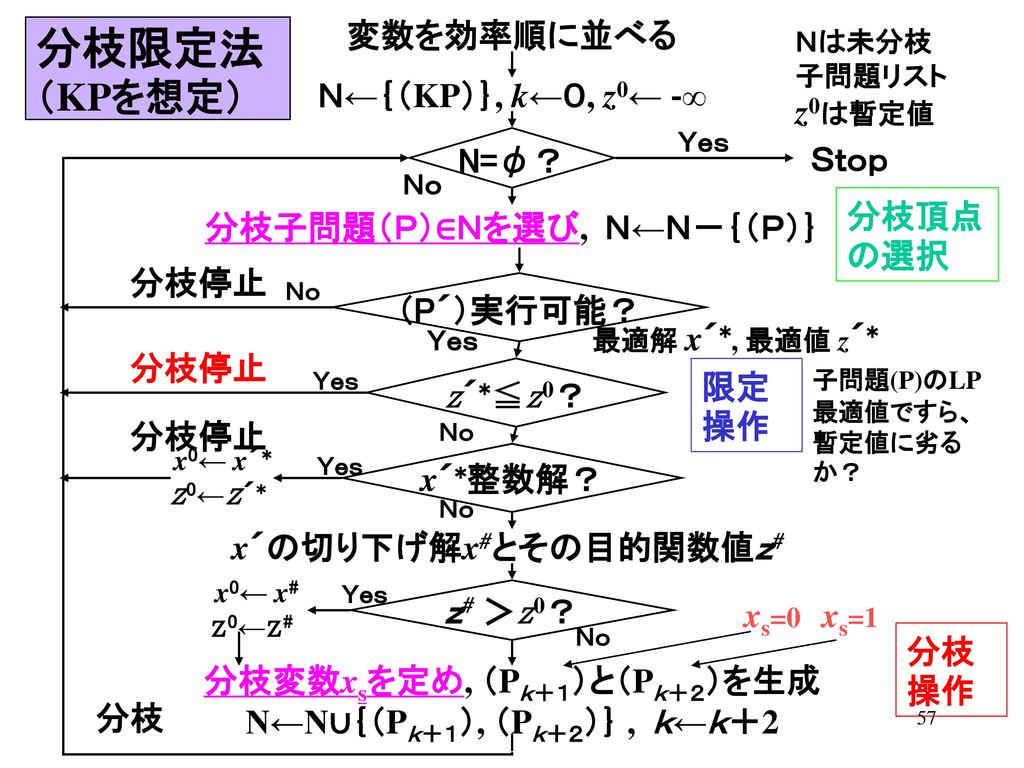
資料1 分枝限定法基礎 第7回: 分枝限定法(2) (スライド) 分枝限定法に基づくナップサック問題の解法 クイズ6 解答 資料1 ナップザック問題の定式化 第8回: ゲーム木における探索法(1) (スライド)解けない問題!? 効率よく解けた⇔(まだ)解けない n製品の最適加工順序問題の場合 最悪計算量 O(nlog 2n) O(n!) n=1万,1億演 算/秒の時 主な解法 機械数 0002秒 6×宇宙年 ジョンソン法 分枝限定法など 2機械 多機械 •効率の良い方法は 見つかっていない分枝限定法の考え方 •問題を場合分けによって部分問題に分解(分枝操作) •01ナップサック問題: 各変数について0 の場合と1 の場合に分ける •分枝の進行の様子は探索木により表現可能 •これだけでは解の全列挙と同じ,時間がかかる

組合せ最適化入門 線形計画から整数計画まで
分枝限定法 ナップサック問題
分枝限定法 ナップサック問題-本記事は、ソフトバンクパブリッシングから発行されている「定本 Cプログラマのためのアルゴリズムとデータ構造 (SOFTBANK BOOKS)」を参考にPythonでアルゴリズムとデータ構造について学習していきます。 今回は、動的計画法によるナップザック問題(Knapsack Problem)について学んでいきます。分枝限定法の考え方 • 組合せ計画問題を,場合分けによって部分問題に分解 (分枝操作) • 01ナップサック問題:各変数について0 の場合と1 の場合に分 ける • 巡回セールスマン問題:次に訪問する都市によって場合分け • 分枝の進行の様子は探索木により表現可能


1 welcome 情報数理研究室 理工学3号館1階北側中央部分 Ppt Download
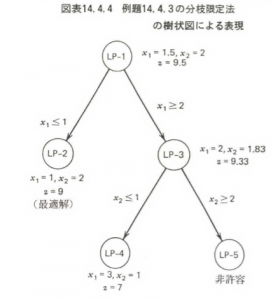
分枝限定法の手順(3)実数最適解を改良して近似最適解(暫定解)を得る ★実数最適解( )1,2/5,0,0 2/5 0 0 1の実数( )を とおき、他の を に置換してみる。 ( )1,0,1,0 →緩和問題の制約式が成立近似最適解Part 4 組合せ最適化,41 節 分枝限定法 pp 補助資料:組合せ最適化短編集(朝倉書店)ナップサック問題(クマさん人形泥棒のお話) Part 4では組合せ最適化の種々の技法を解説 ここでは,01ナップサック問題を例として分枝限定法についてを解説.次のナップサック問題を分枝限定法により解け。 (問題 KP0 )max 15x 118x 26x 32x 4 subject to 4 1 x5x 22x 3x 4 ≦ 6 1, xx 2, x 3, x 4 ∈{0,1} ただし、子問題選択は以下の規則に従うこと。 (1) 奥行優先則 (2) 幅優先則 演習課題 62 次のナップサック問題を動的計画
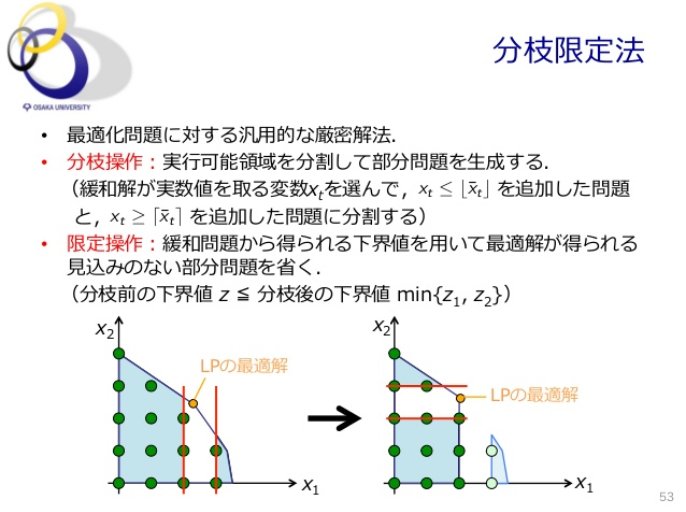
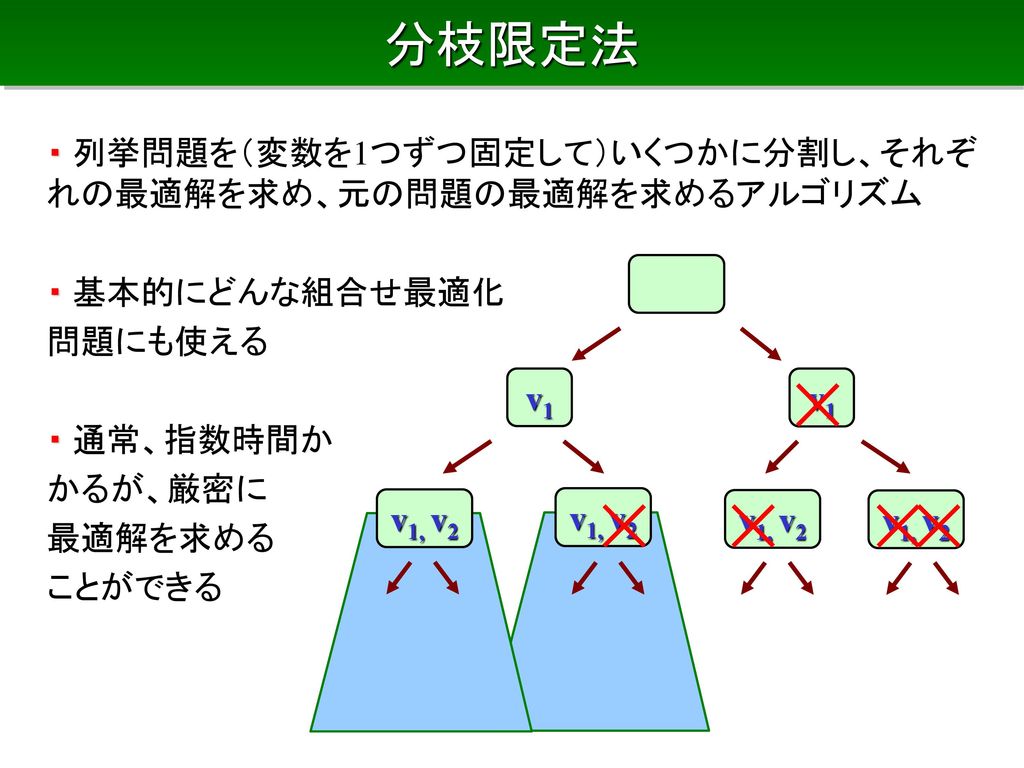
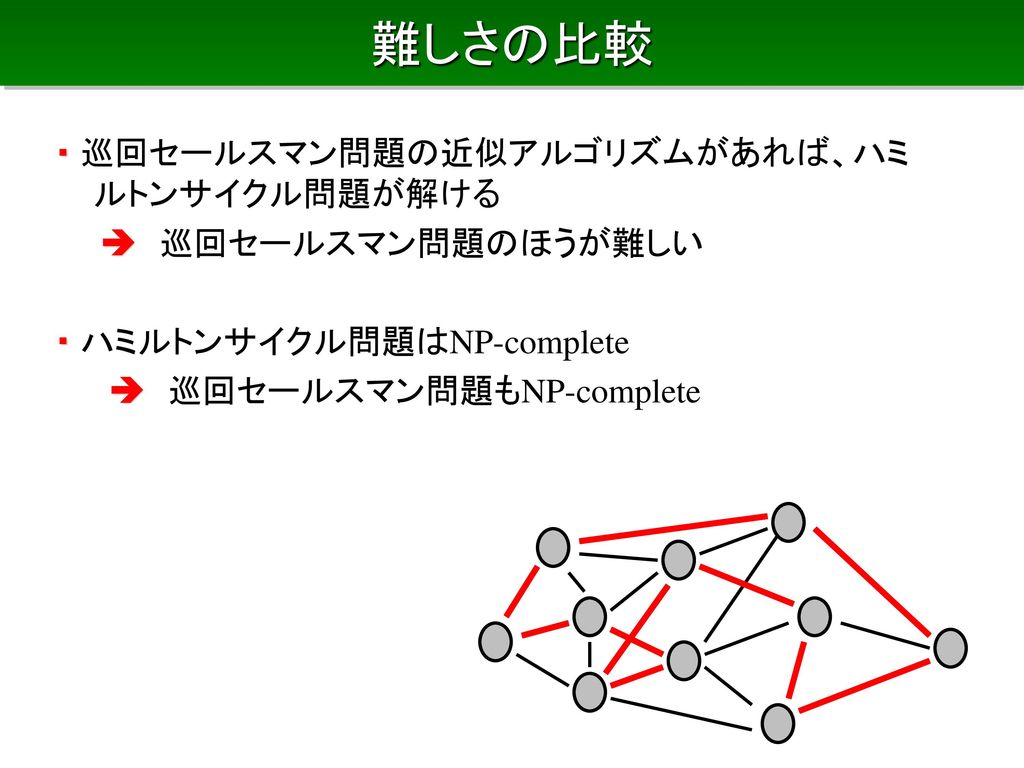
最小木、ナップサック問題、ビンパッキング、巡回セールスマン問題 なる 星型のグラフが最悪(最良)のケース ・ 解の精度がもう少し良くなる 分枝限定法 ・ 列挙問題を(変数を1つずつ固定して)いくつかに分割し、それぞれの最適解を求め、元の解法 分枝限定法(Branch and Bound) まず始めに01ナップサック問題を整数計画問題として定式化します. 整数計画問題 (P) maximize subject to 変数 は値が のとき 番目のアイテムを選択し, のとき選択をしないことに対応しています. 分枝限定法は変数の値を順番に0か1かに固定していき分枝木を;n) ナップサック問題の解は変数の整数条件を外した 線形最適化問題の解とは一般には一致しない 欲張り法も最適解が得られる保証はない
組合せ最適化(くみあわせさいてきか、英 combinatorial optimization 、組み合わせ最適化、または組み合せ最適化とも表記される)は、応用数学や情報工学での組合せ論の最適化問題である。 オペレーションズリサーチ、アルゴリズム理論、計算複雑性理論と関連していて、人工知能、数学、およびナップザック問題(分枝限定法) 目的 ナップザック問題とは、 ここで示すコードは分枝限定法と呼ばれる手法によってナップザック問題を解くコードです。多目的ナップサック問題を解くために動的計画法や分枝限定法をもとにしたアルゴリズム が開発されてきた1 l かしこれらの多くは, 線形なナップサック問題を扱うものであった また, 多次元非線形ナップサック問題においては, これらの手法は有効ではなく,



Atcoder Abc32 D ナップザック問題を分岐限定法で爆速で解く Qiita


ナップサック問題 クマさん人形をめぐる熱いドラマの結末 Ppt Download
分枝限定法(ぶんしげんていほう、英 branch and bound, BB )は、各種最適化問題(特に離散最適化と組合せ最適化)の最適解を求める汎用アルゴリズムである。 分枝操作(英 branching operation )と限定操作(英 bounding operation )から構成される。 全ての解候補を体系的に列挙するもので、最適化さ分列挙法を系統的に繰り返して行う手法が分枝限定法で ある。) ここでは、先ほどの例に対して部分列挙方の考え方を示す。 (1,1,1,1, ,0,02 3 ) x r = 先ほどの、線形緩和で得られた緩和解は、 によって、緩和解の切り捨によって、上界値90を求 めることができ動的計画法(ナップサック問題) 動的計画法とナップサック問題について解説します。 動的計画法とは 直接計算すると大きな時間がかかってしまう問題に対し、途中の計算結果をうまく再利用することで計算効率を上げる手法のこと。



0 1 ナップザック問題について 2 T Nakaの阿房ブログ



大きなナップサック 解説 おじい研究所
分枝限定法の考え方 • 組合せ計画問題を,場合分けによって部分問題に分解 (分枝操作) • 01ナップサック問題:各変数について0 の場合と1 の場合に分 ける • 分枝の進行の様子は探索木により表現可能 • これだけでは,解の全列挙と同じで時間がかかる概要01ナップサック問題を分枝限定法の結果が一致しない。私は今01ナップサック問題を解こうとしています。しかし、出力結果が私の思い描いていたものとは違っておりどうすればよいのかわかりません。 データとしては容量が10のナップサックで入れたいものはそれぞれ、番号0 W = 4 V解けない問題!? 効率よく解けた⇔(まだ)解けない n製品の最適加工順序問題の場合 最悪計算量 O(nlog 2n) O(n!) n=1万,1億演 算/秒の時 主な解法 機械数 0002秒 6×宇宙年 ジョンソン法 分枝限定法など 2機械 多機械 •効率の良い方法は 見つかっていない



Operations Research Yonezawa No2


図で見る分枝限定法 Qiita
11/24 組み合わせ最適化(欲張り法) 12/1 組み合わせ最適化(分枝限定法) 12/8 休講 12/15 グラフとネットワーク(ダイクストラ法) 12/22 グラフとネットワーク(巡回セールスマン問題) 1/12 休講 1/19 ゲーム理論 2/1 試験・最終課題 ナップザック問題ナップサック問題を分枝限定法(Branch and Bound)で解きます。 分枝限定法(ぶんしげんていほう、英 branch and bound, BB)は、 各種最適化問題(特に離散最適化と組合せ最適化)の最適解を求める汎用アルゴリズムである。分枝操作と限定操作から構成される。解けない問題!? 効率よく解けた⇔(まだ)解けない n製品の最適加工順序問題の場合 最悪計算量 O(nlog 2n) O(n!) n=1万,1億演 算/秒の時 主な解法 機械数 0002秒 6×宇宙年 ジョンソン法 分枝限定法など 2機械 多機械 •効率の良い方法は 見つかっていない



1 welcome 情報数理研究室 理工学3号館1階北側中央部分 Ppt Download



Approximation Algorithms For Combinatorial Optimization Problems Speaker Deck
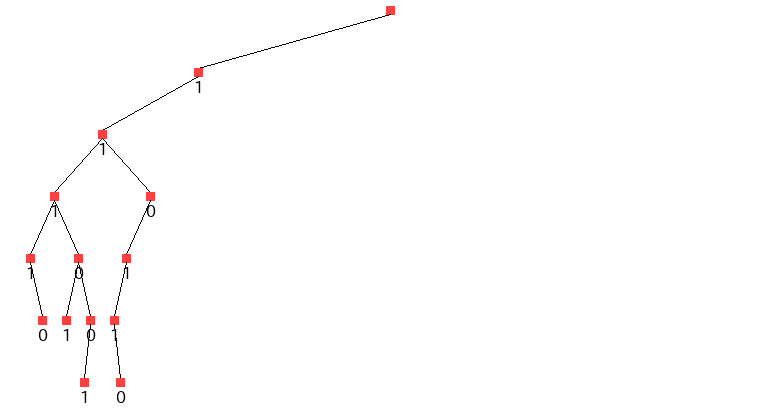
図1 01 ナップサック問題に対する分枝木 31 分枝限定法 分枝限定法は,一部の変数を固定しつつそれぞ れの場合を調べ上げていくという考え方に基づい ている.この過程は,図1 のような図(分枝木と 呼ぶ)を用いて表現できる.一番上の点1は元の分枝限定法 ナップサック問題 最大化z = ∑n i=1 cixi 制約条件 ∑n i=1 aixi b xi 2f0;1g (i = 1;2;分枝限定法の考え方 整数計画問題(組合せ最適化問題)を,場合分けに よって部分問題に分解(分枝操作) 01ナップサック問題:各変数について0 の場合と1 の場合 に分ける 巡回セールスマン問題:次に訪問する都市によって場合分け



ナップサック問題に対する分枝限定法 Youtube



Atcoder Educational Dp Contest D Knapsack 1 ヤマカサの競技プログラミング
生成された部分問題にも反復適用され、探索木(search tree)に示 すように、原問題は次第に小規模な部分問題に分解されていく。 結局、探索木のすべての葉節点の部分問題が解かれ、その結果原問題も 解かれる。 分割統治法と分枝限定法の違い前回 最適化:非線形計画問題のメモ 雑なメモ 最適化:非線形計画問題のメモ 雑なメモ など。ほんとにメモ程度なので、厳密だったりしないし記号の定義などもかなり略、だけど講義の内容は大体ふれてるはず。参考文献、引用文献元は記事末尾参照。 役に立ちそうな文献 中央大学理工分枝操作: ∈0,1のいくつかを固定 緩和:連続化 ∈0,1により解の上界を与える –連続緩和した問題は簡単(𝑞 / が大きい方から詰めるだけ) 分枝限定法の別の例: ナップサック問題



知能情報処理 第1回 この授業の概要 組合せ最適化問題とは Ppt Video Online Download


Y S R ら ぶ ぱ ぴ 完 走 し ま し た アルペで分かる 整数計画法5 伊400 だが手がないわけではない Ip問題に有効な手段の一つとして 分枝限定法がある 伊402 困難は分割せよ 分枝 限定操作によって 最適解の範囲を順次狭めていくこと
グラフ探索問題 • 頂点v ∈V に対してそれと辺でつながれた頂点の集合を T(v) とする. • グラフ探索問題:出発点となる頂点v0 と関数T とが与えられ たときすべての頂点を列挙する問題 – 分枝限定法では,関数T の返値は分枝操作により得られる頂点 • 基本的な戦略:図1 01 ナップサック問題に対する分枝木 31 分枝限定法 分枝限定法は,一部の変数を固定しつつそれぞ れの場合を調べ上げていくという考え方に基づい ている.この過程は,図1 のような図(分枝木と 呼ぶ)を用いて表現できる.一番上の点1は元のPart 4 組合せ最適化,41 節 分枝限定法 pp 補助資料:組合せ最適化短編集(朝倉書店)ナップサック問題(クマさん人形泥棒のお話) Part 4では組合せ最適化の種々の技法を解説 ここでは,01ナップサック問題を例として分枝限定法についてを解説.



B 2 3 分枝限定法


組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download



組合せ最適化


図で見る分枝限定法 Qiita


基礎or or演習 第6回 11 17 09 森戸担当分中間試験 来週 11 24 火 13 00は試験 Ppt Download


4 4 離散形最適化のアルゴリズム ものづくり のためのjmaオンラインセミナー 日本能率協会



1995 号 最適解探索方式および最適解探索方法 Astamuse


第2回 ナップサック問題を色々な方法で解いてみた ブレインパッドの数理最適化ブログ Platinum Data Blog By Brainpad


組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download



組合せ最適化



組合せ最適化入門 線形計画から整数計画まで



第2回 ナップサック問題を色々な方法で解いてみた ブレインパッドの数理最適化ブログ Platinum Data Blog By Brainpad



混合整数線形計画法 Mip アルゴリズム 入門



組合せ最適化


組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download



組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download



Python ナップザック問題を分枝限定法 Branch And Bound で解く Qiita



組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download


知能情報処理 第1回 この授業の概要 組合せ最適化問題とは Ppt Video Online Download



組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download
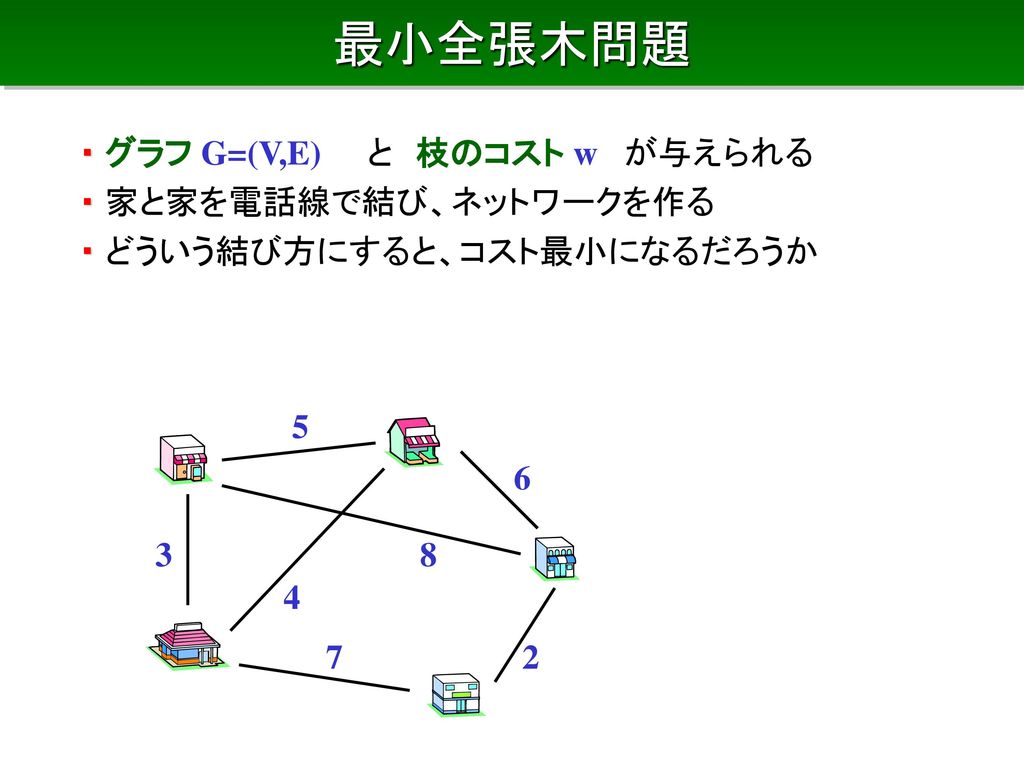


組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download



Ppt 情報システム基盤学 基礎 1 アルゴリズムとデータ構造 Powerpoint Presentation Id



動的計画法 ナップサック問題 アルゴリズム講習会


知能情報処理 第1回 この授業の概要 組合せ最適化問題とは Ppt Video Online Download



第2回 ナップサック問題を色々な方法で解いてみた ブレインパッドの数理最適化ブログ Platinum Data Blog By Brainpad



問題解決力を鍛える アルゴリズムとデータ構造 書籍情報 株式会社 講談社サイエンティフィク



知能情報処理 第1回 この授業の概要 組合せ最適化問題とは Ppt Video Online Download



Mathematical Optimization In 60 Minutes Speaker Deck
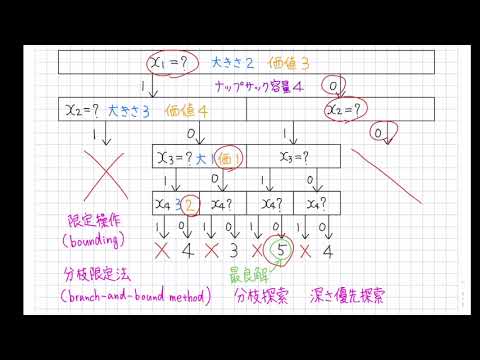


ナップサック問題に対する分枝限定法 Youtube
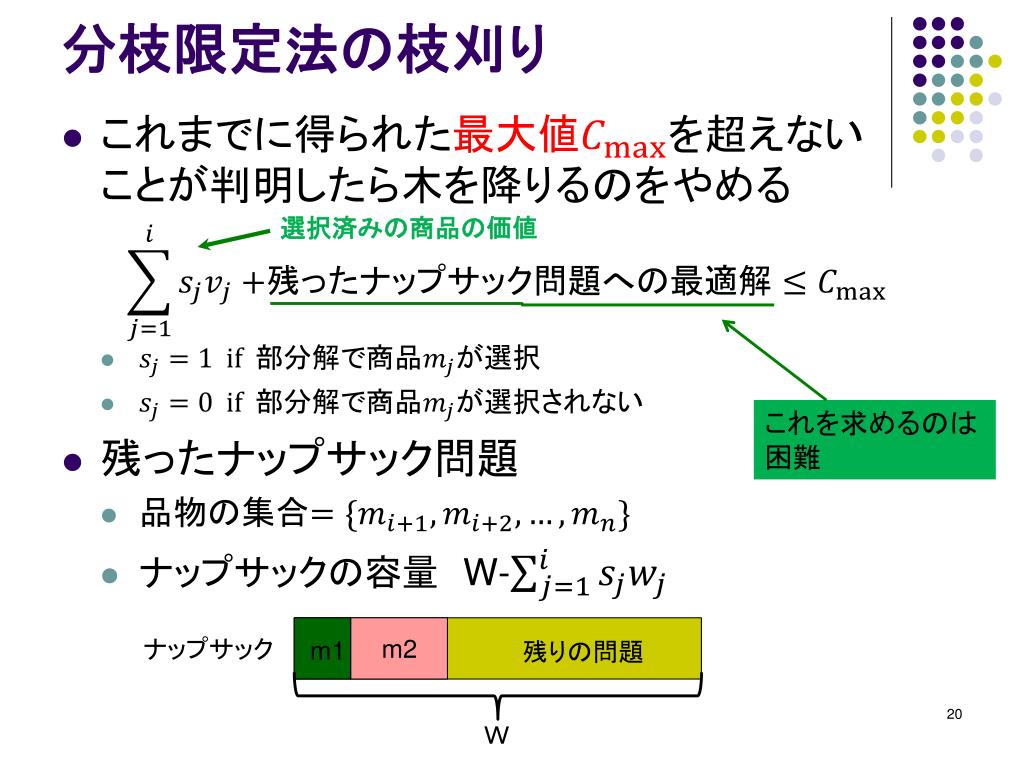


Ppt 情報システム基盤学 基礎 1 アルゴリズムとデータ構造 Powerpoint Presentation Id
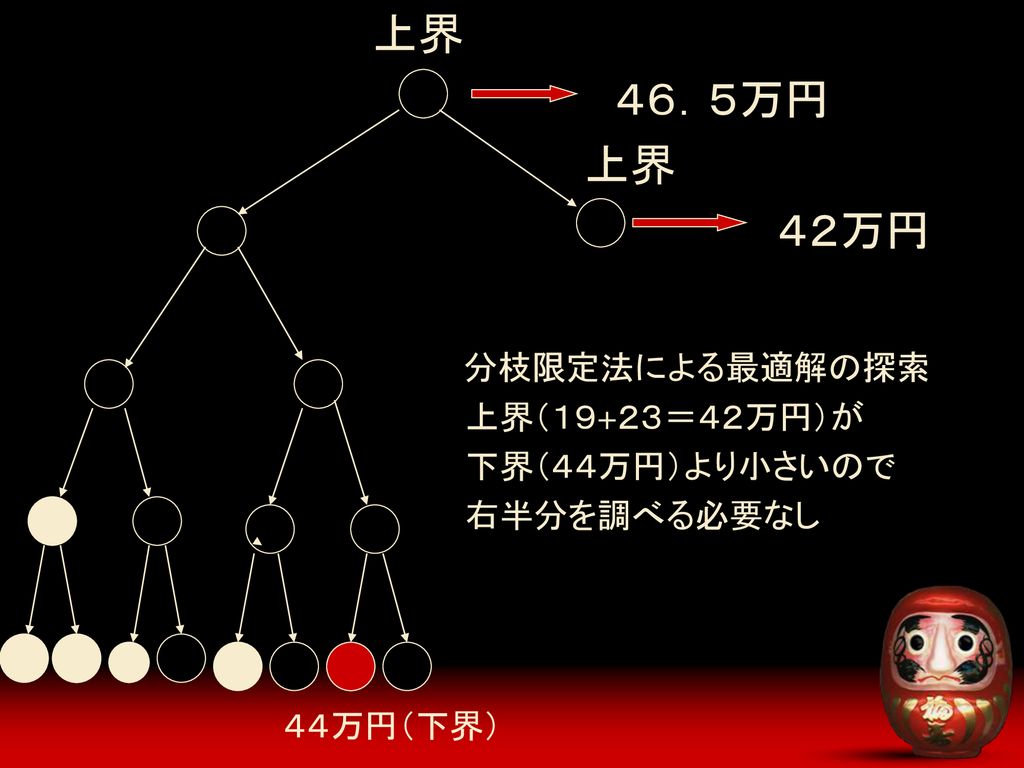


ナップサック問題 クマさん人形をめぐる熱いドラマの結末 Ppt Download



組合せ最適化入門 線形計画から整数計画まで


7 3 分枝限定法の並列化の利用



7 3 分枝限定法の並列化の利用
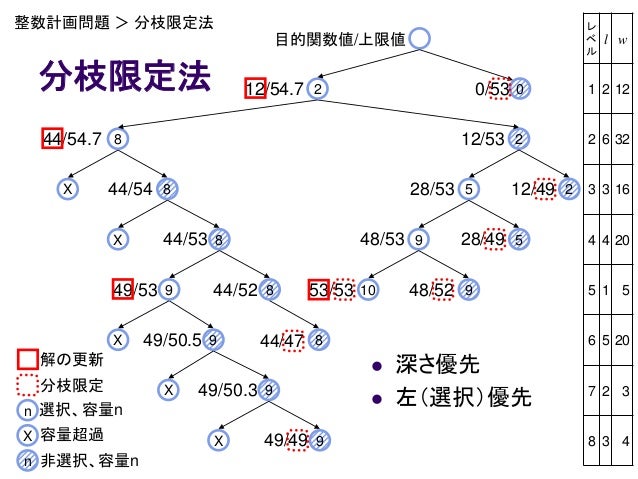


Operations Research Yonezawa No2
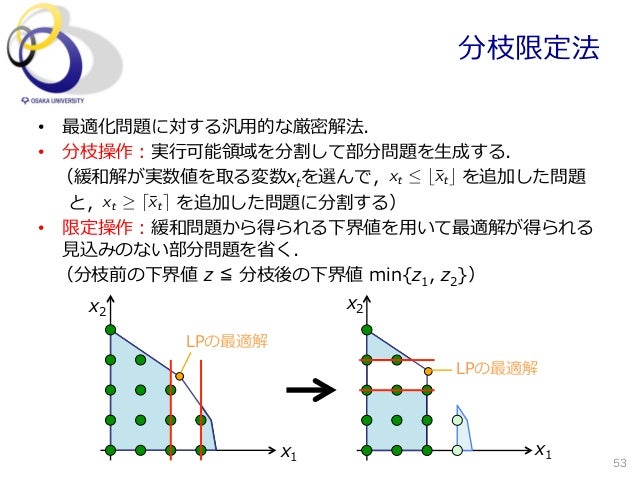


組合せ最適化入門 線形計画から整数計画まで



組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download



大きなナップサック 解説 おじい研究所



04 号 問題分割方法 最適化方法 問題分割装置 最適化装置 及びコンピュータプログラム Astamuse


7 3 分枝限定法の並列化の利用



情報工学概論 アルゴリズムとデータ構造 09動的計画法01ナップサック問題01問題設定と用語 Youtube



組合せ最適化



1995 号 最適解探索方式および最適解探索方法 Astamuse



Python 分枝限定法でナップサック問題を解く Qiita
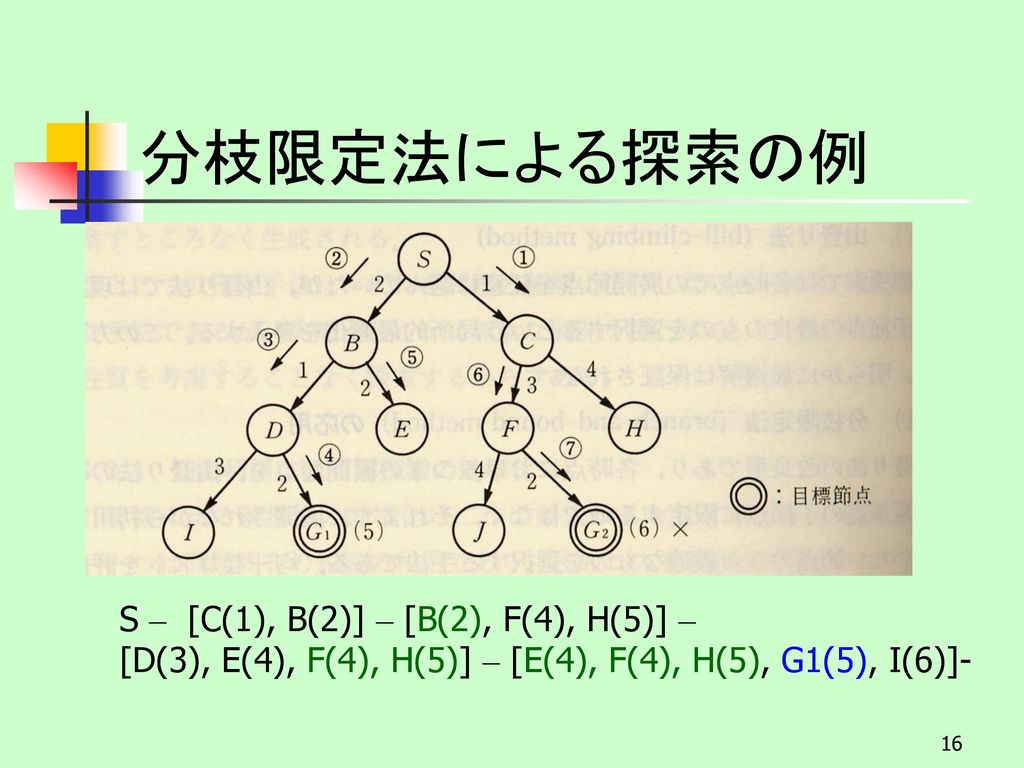


第8回 問題解決 Ppt Download



組合せ最適化問題と厳密解法 最小木 ナップサック問題 ビンパッキング 巡回セールスマン問題 Lpによる上界 下界 分枝限定法 Ppt Download



1995 号 最適解探索方式および最適解探索方法 Astamuse



B 2 3 分枝限定法



Atcoder Abc32 D ナップザック問題を分岐限定法で爆速で解く Qiita
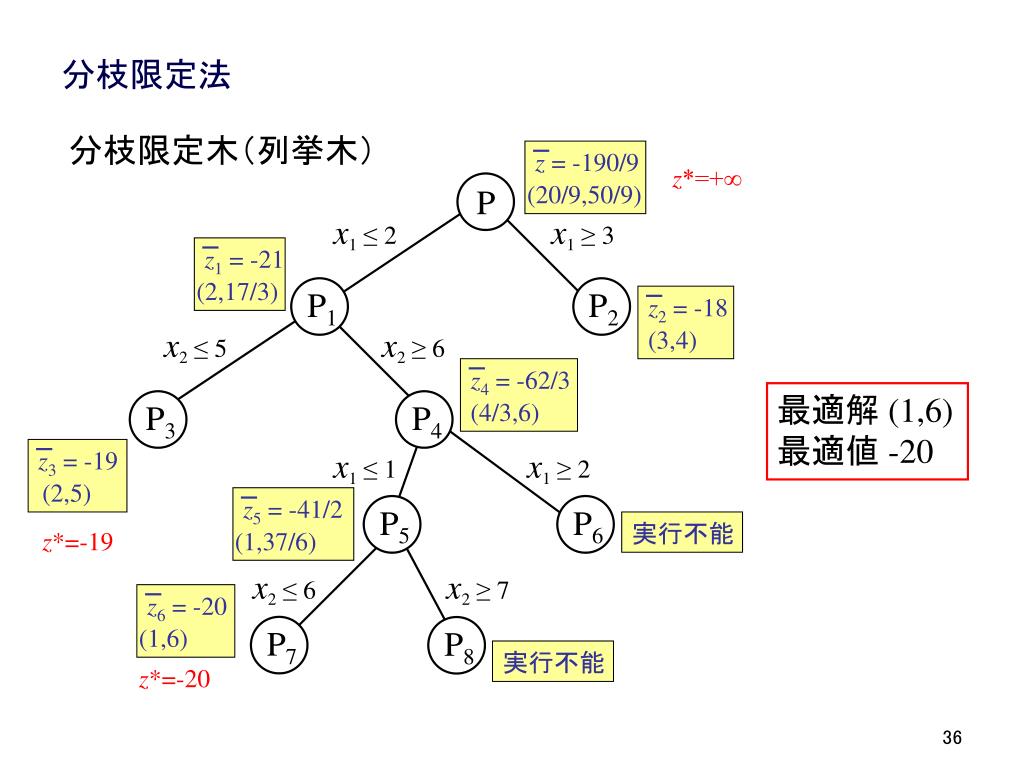


Ppt 最適化ワークショップ 整数計画法の発展と応用 整数計画法チュートリアル モデリングと解法 Powerpoint Presentation Id



Ppt 最適化ワークショップ 整数計画法の発展と応用 整数計画法チュートリアル モデリングと解法 Powerpoint Presentation Id



ナップサック問題の分枝限定法 Likeな最適化操作をjumpを使って動作確認する



1995 号 最適解探索方式および最適解探索方法 Astamuse



ソフトウェアii 第4回 12 10 ソフトウェアii



情報工学概論 アルゴリズムとデータ構造 09動的計画法01ナップサック問題01問題設定と用語 Youtube
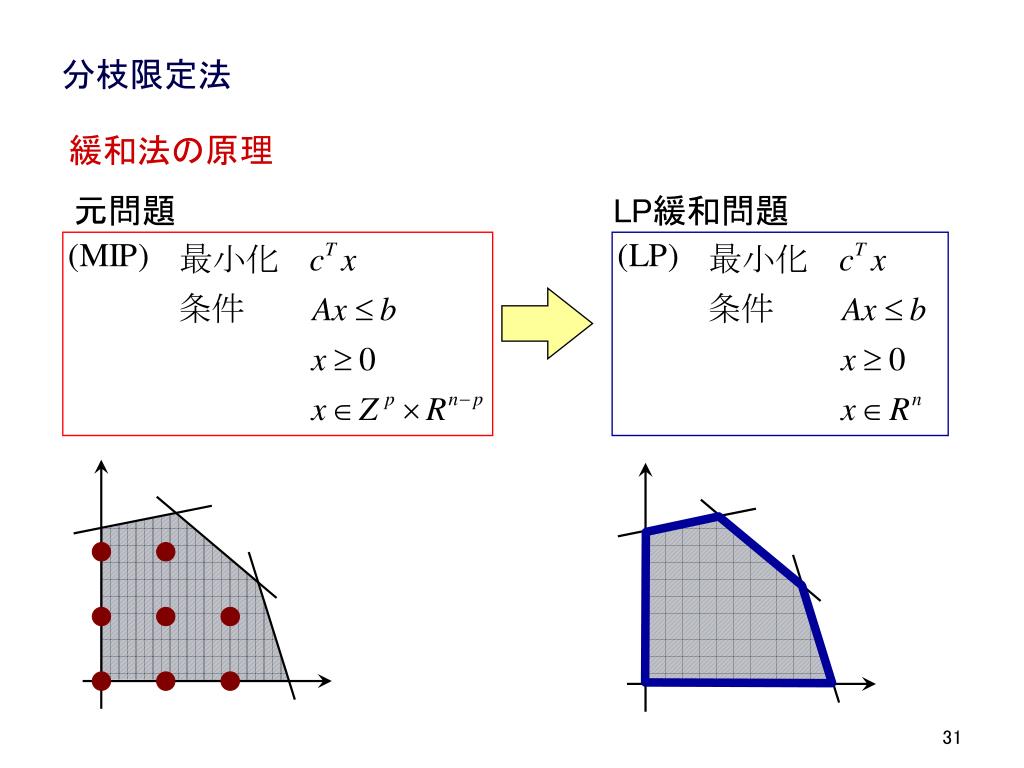


Ppt 最適化ワークショップ 整数計画法の発展と応用 整数計画法チュートリアル モデリングと解法 Powerpoint Presentation Id



組合せ最適化


資材切出し問題と列生成法



Mathematical Optimization In 60 Minutes Speaker Deck
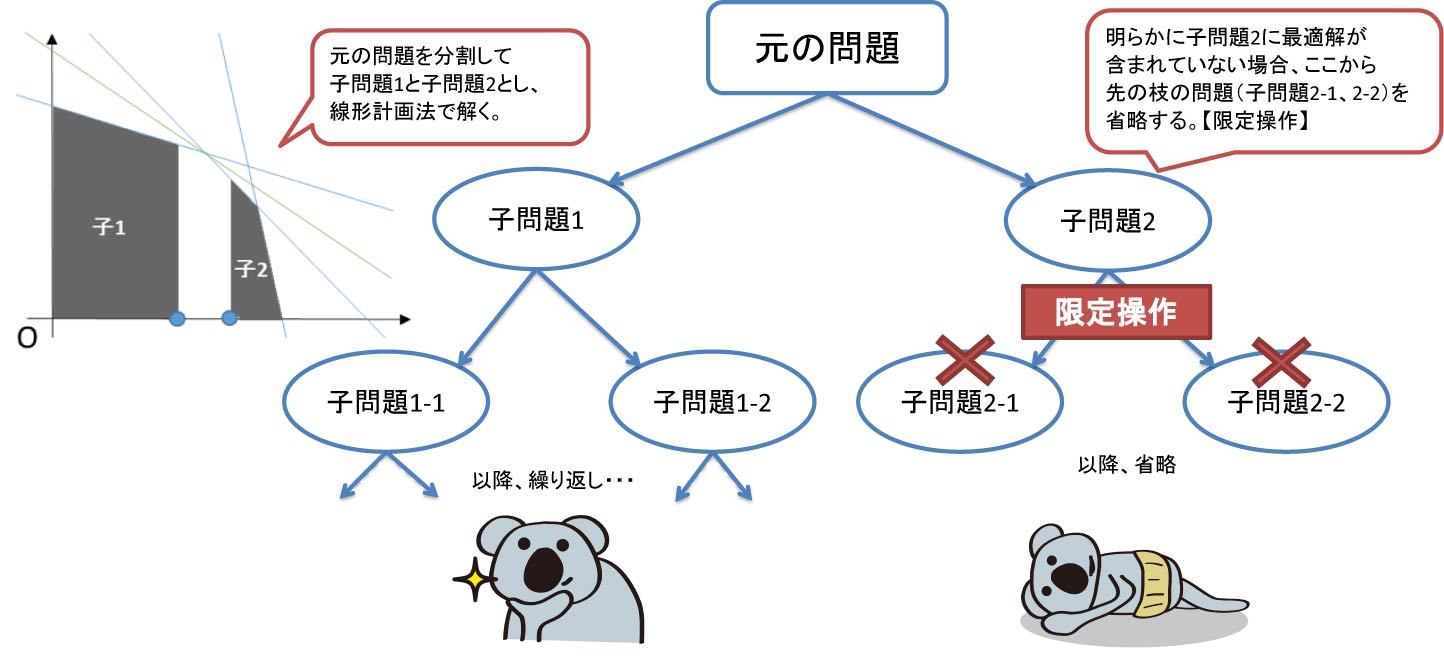


連載コラム 数理最適化 第5回 数理最適化とその歴史 貴社ビジネスのit共創者 中央コンピューター株式会社


大きなナップサック 解説 おじい研究所



0 件のコメント:
コメントを投稿